À la fin du Dom Juan de Molière (acte V, scène III), un spectre sous forme de femme voilée se présente devant Dom Juan et Sganarelle. Ce dernier, assez inquiet, alerte son maître, car cette apparition est à ses yeux une mise en garde venue du ciel. Dom Juan ne se laisse pas intimider : « Spectre, fantôme, ou diable, je veux voir ce que c’est. »
Depuis l’introduction par Newton de « spectre » dans les sciences exactes, se référant au « spectre coloré » qu’il avait observé en faisant passer la lumière du soleil dans un prisme, le mot a perdu, chez les scientifiques, sa connotation surnaturelle. Il est resté, néanmoins, un objet qui interroge les chercheurs et surtout les mathématiciens, ce qui conserve son actualité au propos de Dom Juan. Les spectres, depuis Newton, posent une question clé : celle de la relation entre la nature apparemment continue des phénomènes et leur structure sous-jacente discontinue ou discrète, comme préfèrent dire les mathématiciens. En mathématiques, nous rappelle Nalini Anantharaman, le champ de bataille, jamais vraiment pacifié, entre discret et continu est incarné par l’opposition entre l’ensemble des nombres entiers et celui des nombres réels.

La « géométrie spectrale », objet de la chaire du Collège de France dont Histories de spectres est la leçon inaugurale, est l’étude de la décomposition des solutions d’équations différentielles, continues dans leur nature, dans un nombre fini ou infini d’entités pouvant être discrètes. L’adjectif « spectrale » pour se rapporter à la détermination des modes propres d’un opérateur différentiel fut utilisé en premier lieu par David Hilbert au début du XXe siècle. Pour recourir à une analogie physique, on sait que la corde d’un violon possède des fréquences de vibration qui dépendent de la longueur de sa partie vibrante, de sa masse linéique (masse par unité de longueur) et de la tension. L’accordeur ajuste la tension de chaque corde pour que ses modes de vibration soient ceux désirés. Pour jouer, le violoniste modifie la longueur de la partie libre de la corde en la pinçant de ses doigts. Le spectre de l’équation différentielle décrivant la corde représente l’ensemble de ses modes de vibration. L’équation différentielle étant linéaire, toute vibration de la corde sera le résultat d’une combinaison des modes propres qui composent son spectre.
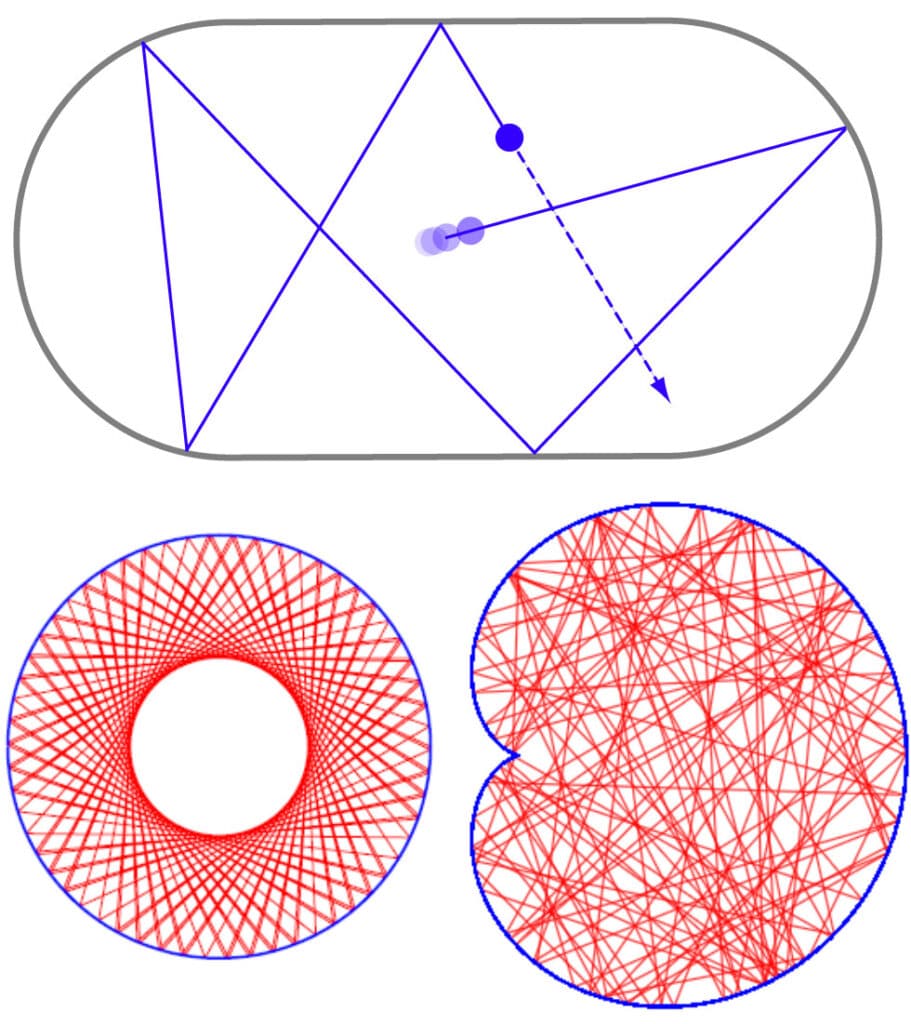
Le cœur des recherches de Nalini Anantharaman, qui lui ont valu, entre autres, le prix Henri-Poincaré en 2012 et la médaille d’argent du CNRS l’année suivante, est l’étude du spectre de systèmes dynamiques. On appelle « dynamique » un système dont l’évolution en fonction du temps est décrite par une équation différentielle telle que, par exemple, la loi de Newton ou celle de Schrödinger. Au-delà des spectres, la chaire du Collège de France a pour titre « géométrie spectrale » ; pourquoi « géométrie » ? Pour le comprendre, il faut faire appel à une autre représentation assez évocatrice d’un système dynamique et de son spectre. Il s’agit de ce qu’on appelle un « billard dynamique ». On imagine une particule dont les trajectoires sont définies par une équation du mouvement, celle de Newton par exemple. La particule se déplace librement sur une surface délimitée par des bords sur lesquels elle rebondit de façon parfaitement élastique. Dans certains systèmes dynamiques, dénommés intégrables, les trajectoires démarrant selon des conditions initiales très proches entre elles évoluent ensemble, traçant des figures dans l’espace qui en couvrent des portions bien définies et limitées. C’est le cas du billard circulaire (représenté dans la figure en bas à gauche), ou bien d’un système newtonien à deux corps (le système Terre-Lune, en négligeant l’effet du soleil et des autres planètes, en est un exemple).
Les trajectoires d’autres systèmes, dits chaotiques, divergent entre elles de manière exponentielle, à l’égard du du temps. Cela fait que même des trajectoires aux conditions initiales infiniment proches s’éloignent très rapidement les unes des autres, l’ensemble des trajectoires recouvrant d’une manière presque uniforme tout le système. C’est le cas du billard cardioïde (figure en bas à droite), ainsi que du stade de Bunimovich (figure en haut). On voit, depuis les exemples présentés, que la géométrie du billard détermine la nature des trajectoires et donc de son spectre. Tandis que les trajectoires d’un système intégrable peuvent être calculées de façon exacte, l’extrapolation de celles d’un système chaotique est une tâche bien plus problématique. Pour les physiciens, savoir extrapoler les spectres des systèmes chaotiques de manière exacte ou approchée est une priorité, vu leur omniprésence dans la nature. Depuis Poincaré, on sait que, sur une grande échelle de temps, même le système solaire est chaotique. Il en est de même pour la plupart des atomes complexes (lourds). Pour les mathématiciens, démontrer des relations entre géométrie, voire topologie, de l’espace des phases des systèmes dynamiques, et les propriétés de leurs spectres est un problème qui accompagne celui de leur compréhension.
Dans la suite de la leçon, l’autrice mentionne quelques-uns des domaines qui font l’objet de ses recherches et dans lesquels elle a publié des résultats marquants. Entre autres, le chaos quantique. Il s’agit de l’étude de systèmes dynamiques chaotiques régis par l’équation de Schrödinger. Déjà Einstein, en 1917, s’intéressa à la recherche du spectre de ce type de systèmes. Depuis 1955, on sait que certains d’entre eux possèdent un spectre impossible à calculer de façon exacte, mais équivalent de celui d’une matrice aléatoire de grande taille. En 1984, s’appuyant sur trois décennies d’expériences, une relation directe entre matrices aléatoires et chaos quantique fut postulée par la « conjecture de Bohigas-Giannoni-Schmit » ; malheureusement, une démonstration rigoureuse de cette hypothèse n’a pas encore été formulée.
Le livre se poursuit par une discussion sur le lien entre les spectres de l’opérateur différentiel de Laplace, omniprésent dans les équations des ondes, et les propriétés topologiques des surfaces sur lesquelles l’opérateur agit. Finalement, l’autrice mentionne brièvement les problèmes dits « inverses » où l’on cherche à reconstruire la géométrie d’un système à partir de la connaissance de son spectre. Il s’agit de la question posée en 1966 par Mark Kac, l’un des grands mathématiciens du XXe siècle : « peut-on entendre la forme d’un tambour ? ».
Comme le dit Nalini Anantharaman, en mathématiques démontrer est synonyme de comprendre et c’est à ce type de compréhension qu’elle consacre toutes son énergie.
Par sa façon d’expliquer, claire, attentive à la possibilité d’apprendre à partir des difficultés et même des erreurs, Nalini Anantharaman fait preuve d’une sensibilité rare chez les savants de son calibre. Son style met en avant la créativité sans jamais manifester cette agressivité intellectuelle qu’on associe au génie, surtout chez les mathématiciens et les physiciens. Lire son beau livre ou assister à sa leçon inaugurale, disponible sur le site du Collège de France, pourra servir au public de remède contre la « peur des mathématiques » qui trop souvent éloigne les jeunes des sciences exactes.
Ceux qui voudraient se familiariser avec les origines de la théorie du chaos pourront aussi lire la transcription d’une conférence d’Étienne Ghys qui vient d’être publiée dans la collection « Les grandes voix de la recherche » des éditions du CNRS. L’auteur, mathématicien, médaille d’argent du CNRS en 1991, lauréat en 2022 avec Julien Bobroff, Carolyn Scheurle et Jean-Claude Ameisen de la médaille de la médiation scientifique du CNRS, y examine brièvement et avec clarté l’histoire de la notion de chaos, depuis Poincaré jusqu’au fameux « effet papillon » associé à l’attracteur de Lorenz.












